


Hints for teachers and parents about the rational learning of the multiplication table
We use multiplication everyday without realizing it.
Multiplication is used to determine the size or number of elements in many
groups of equal size. For example, there are 6 candies in a pack and you
buy 4 packs, how many candies do you have altogether? This problem can be
solved by addition as follows: 6+6+6+6 = 24. This method is known
as repeated addition and it can be replaced by the multiplication method
4*6 = 24 . This is one interpretation of multiplication in which
multiplication problems involve a number of sets (e.g. 4 packs of candies),
each having the same number of objects (e.g. 6 candies per pack). The relation
between the repeated addition and multiplication methods clearly shows the necessity
of mastering elementary addition before learning the 10 x 10 multiplication
table.
Multiplication is also used to determine the number of
objects that are arranged in an array. An array is an arrangement of objects
in a number of equal sized rows or columns. You can observe many arrays in
a supermarket such as cans on the shelves. The Fig. 1 below shows there
are four rows of cans with six cans in a row or six columns with four cans
in a column.
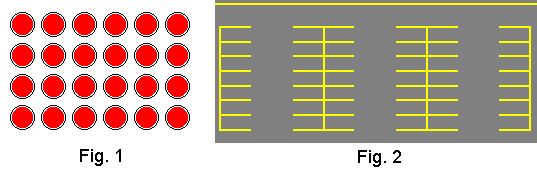
This may be interpreted as a 4x6 array with four rows
and 6 cans in each row or as a 6x4 array with six columns and 4 cans in each
column.
The following problem illustrates the use of the array interpretation of
multiplication. There are 6 rows of parking spaces in a parking lot and each
row can park 7 cars (see Fig. 2 above), how many cars can be parked in the
parking lot? The multiplication method gives us 6*7 = 42.
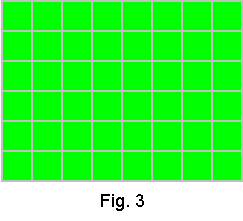
Another interpretation that relates to the array model
is the area model. A typical question to illustrate this model is: A metal
sheet is 6 feet by 8 feet, what is the area of the sheet. The answer can
be easily found from Fig. 3.
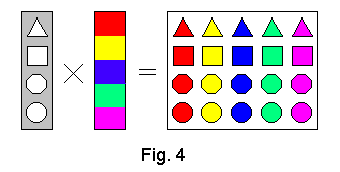
Multiplication is also related to the Cartesian product of
two sets. Imagine a rectangular plate with four cut out shapes: triangle,
square, octagon and circle. Let us treat it from mathematical point of view
as a set of four shapes. Another set is a box with five cans of paint: red,
yellow, blue, green and violet. Formally a Cartesian product of any two sets
is defined as a third set containing all different pairs of elements created
by taking one element from the first set and one element from the second
set. In Fig. 4 there are presented all these sets and operation of making
a Cartesian product is marked with "X" (notice that the same symbol "X" is
also used to mark multiplication of two numbers, but then it has a totally
different meaning). You can see the outcome of this operation represents
the set of all shapes from the first set paired with all colors from the
second set. All together 20 elements of the third set that differ by shape, color
or both, shape and color. The number of elements of the third set can be
obtained by multiplication of the number of elements in the first set by
the number of elements in the second set.
Take another problem of this sort. There are 5 boys and
4 girls at a party. How many different dancing partners can be formed? In
abstract terms we have solved this problem already. To see this, it is enough
to realize that we can assign to each boy a different shape from the former
problem utilizing all shapes and to each girl a different color utilizing
all colors from the former problem.
There are many problems in real life in which the Cartesian
product model of multiplication is used. For example, different packages
to be wrapped from a given number of colors of wrapping paper and differently
colored ribbons. The number of outfits that can be arranged using a given
number of skirts and blouses, shirts and pants. The number of different meals
from a given number of different items like meats, salads, vegetables, and
drinks.
Learning the basic interpretations of multiplication is necessary for knowing
when and how to use multiplication solving real problems such as these presented
above. These interpretations are also very helpful in a rational learning
of the 10 x 10 multiplication table in elementary education. Later on they
help to understand some of the following formal axiomatic properties of
multiplication:
1. a*0 = 0*a = 0
the zero property
2. a*1 = 1*a = a
the identity property
3. a*b = b*a
the commutative property
4. a(b+c) = ab+ac the distributive
property.
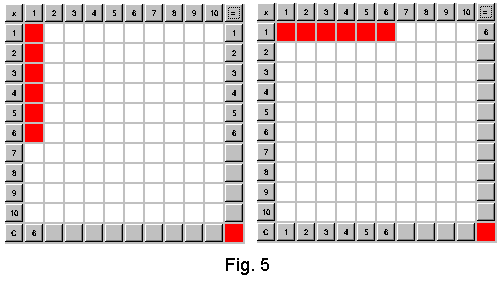
The array interpretation of multiplication explains all
of these properties. Taking a times (e.g. six times) a row containing
no elements (zero elements) or zero times a row containing a elements leaves
us with no elements. This is just what the zero property states. The same
line of arguments applies to the identity property. This time, however, a
times a row containing one element or one times a row containing
a elements should be taken. For the identity property all of it is demonstrated
in Fig. 5 presenting two instances of our visual multiplication table.
The comutativity property is illustrated a similar way in Fig. 6. It is visually clear there that 4*9 gives the same number of blue squares as 9*4.
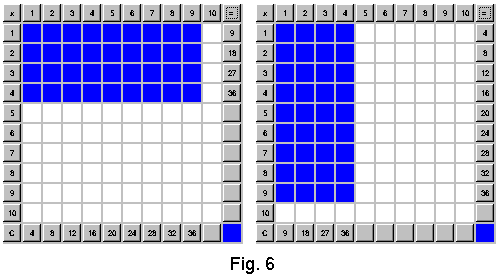
The distributive property can also be illustrated with the
help of Fig. 6. It can be seen from this figure what does it mean that 4*9
= (2 + 2)*9 = 2*9 + 2*9 = 18 + 18 = 36. Thus, if somebody knows how much
is 2*9 then to find how much is 4*9 this person has to add
eighteen and eighteen. Looking on Fig. 6 one can see another method of quick
finding the resultant of 4*9. It goes like this 4*9 = 4*(10 - 1) =
4*10 - 4*1 = 40 - 4 = 36.
These examples show how it is possible to master the
multiplication table learning about its interpretation, structure and properties
rather than memorizing it. This kind of approach sets a good background for
learning and understanding more sophisticated math.
Other related places
Natural Math
Counting Game

